傅里叶级数和傅里叶变换
傅里叶级数和傅里叶变换
作为一名信息与通信工程专业的本科生,傅里叶先哲的大名小弟早已久仰万分。(主要是一开始被傅里叶级数和变换的数学表达式按在地上摩擦。好不容易高数学完了吧,没想到又在专业课上碰到了……)
傅里叶级数
傅里叶级数表明:任何周期函数都可以用正弦函数和余弦函数构成的无穷级数来表示(正弦函数和余弦函数相互正交)。也就是说,不论一个周期信号有多么复杂、长得多么奇怪,它都可以被由不同个正弦函数和不同个余弦函数表达出来。
举个例子,下图这样一个信号就可以分解为另两个信号(正弦、余弦)之和

目前,我们处于一般状态下的信号——时间坐标系,即时域下。当我们换个角度,即信号——频率坐标系(频域)下,这些图像又会发生什么样的变化呢。

不难看出,投影到频域上的信号图像是离散的非周期的线段,这里的自变量频率也就是一个标准正弦信号表达式y=Asin(wt+θ)中的w。
那么有了w的频谱,θ又在哪里呢?别着急,下面这幅图会给你一个答案。

向下投影,我们可以得到在不同w下的不同θ值(一般取相位的主值范围为 (-π, π])
傅里叶变换
刚才,我们谈傅里叶级数是针对“周期”且”连续”的信号而言,得到的是“非周期”且“离散”的频谱。
而自然界中的非周期信号也琳琅满目,对于它们,就需要用上傅里叶变换了。

这里,上方对应的是傅里叶级数,下方对应的是傅里叶变换。不难看出,对于傅里叶变换,时域信号是“非周期”且“连续”的,而变换后的频域信号则为“非周期”但“连续”的,与傅里叶级数对应不同。
| 时域 | 频域 | |
|---|---|---|
| 傅里叶级数 | 周期、连续 | 非周期、离散 |
| 傅里叶变换 | 非周期、连续 | 非周期、连续 |
数学表达
傅里叶级数
傅里叶级数公式:
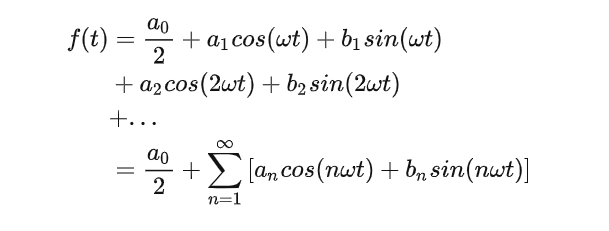
其中,
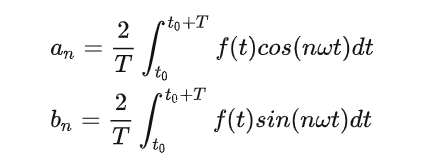
傅里叶变换
f(x)从时域到频域F(w):
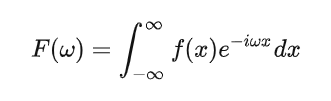
从频域F(w)到时域f(x):
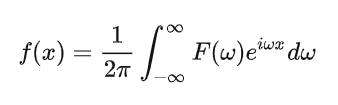
到这里,一些有关傅里叶级数及傅里叶变换的初级内容就介绍完啦,感谢你们的收看,更多相关的性质我们留在下一p去讨论。在此贴一个比我科普详细一百倍的网站链接,大家还有什么不太理解和清楚的地方可以去这里借鉴:深入浅出的讲解傅里叶变换(真正的通俗易懂)_后脑勺的博客-CSDN博客_傅里叶变换,我们下期再见啦~





